" 'They' Isn't Singular!" Oh Yeah? Show Me Its Multiplicative Inverse Matrix Then.

" 'They' isn't singular!" Oh yeah? Show me its multiplicative inverse matrix then.

types of mathematical terminology

descriptive

honeycomb

gradient

quiver

computable

less descriptive

centroid

chaos

end

flag

not descriptive

ring

allegory

surreal

group

you know this person, right?

euclidean

abelianization

grothendieck

cartesian

took some non-english word and hoped for the best

eigen

algebra

shtuka

nullstellensatz

i made up a word!

ergodic

functor

adele

logarithm

idk, just give it a generic name

regular

well

admissible

well-admissible

like, specifically, it’s a vague thing

flasque

lax

fuzzy

pseudo

one symbol and a word

*-algebra

D-module

K-theory

†-compact (although that’s going to usually be written “dagger compact”)

just random letters

rg

cwf

Fσ

erf

10-12 VIII 2021

finished the basics of the measure theory and god am i in love

sleep: ok

concentration: good

phone time: good

yeah so now i know what a measurable set and a measurable function is, i'm on my way to lebesgue integration. however, i don't have the intuition for measurable functions yet, just the basics. there are those two theorems that i merely vaguely understand and idk barely can touch them. one of them is lusin, the other one is frechet. they seem very important as they deal with continuity of a function in the context of measurability. and do we love continuous functions my dude yes we do

tomorrow i plan to solve some problems concerning measurable functions and then do topo. i must admit, measure theory devoured me entirely recently and i had a break from topo. gotta fix that. and possibly do some coding

6 Things People Don't Always Tell You About Studying

1. you ace tests by overlearning. you should know your notes/flashcards/definitions basically by heart. if someone asks you about a topic when you’re away from class or your notes and you can answer them in a thorough and and accurate answer, then you’re good, you know the material. 

2. if you don’t understand something, it will end up on the test. so just don’t disregard and hope that this specific topic won’t be on the test. give it more attention, help, and practice. find a packet of problems on that one concept and don’t stop until you finish it and know it the best. 

3. sometimes you just need that Parental Push. you know in elementary school, they would tell you “ok now it’s time for you to do your homework! you have a project coming up, start looking for a topic now!” ONE of your teachers might be like this. be thankful for it and follow their advice! these teachers are the best at always keeping you on track with their calendar. if not a teacher, then have one of your friends be that person that can keep you accountable for the things you promised you would do. 

4. you just need to kick your own ass. seriously. i know it sucks and its hard to study for two things at once. BUT. I DONT CARE IF IT’S HARD. you need to do it and at least do it to get it over with because you can’t keep putting things off. If you do, you will eventually run out of time and you will hate yourself. force yourself to do it. i made myself sign up for june ACT even though there’s finals because if i didn’t, i probably never would. like do i think i’m gonna be ready in one month? probably not, SO I BETTER GET ON IT AND START STUDYING! 

5. do homework even if it doesn’t count. if you actually try on it, then you will actually do so much better on the tests, it’s like magic. 

6. literally just get so angry about procrastinating that you make yourself start that assignment. I know how hard it is to kick the procrastination habit. I have to procrastinate. So I make myself start by thinking about my deadlines way early. I think, “oh i have a presentation in three weeks (but it really takes 2 weeks to do), i’ll be good and start today.” when that doesn’t happen, you say you’ll do it tomorrow, and this happens for like the next four days. I get so mad at myself for not starting when i am given a new chance to do so with every passing day. By that time, you actually have exactly how much time you need for it AND you were able to procrastinate the same way you usually do ;)

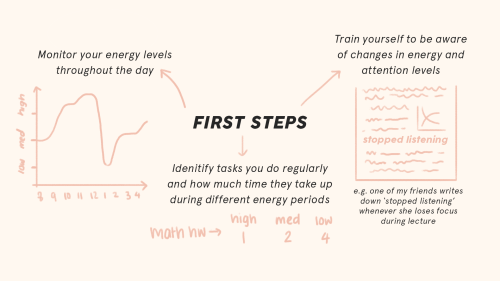
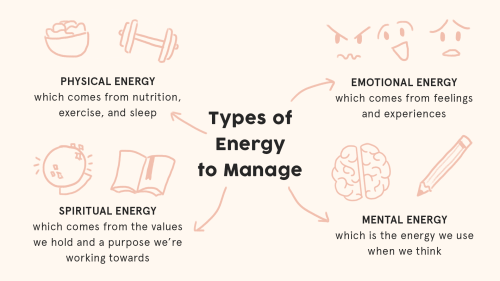
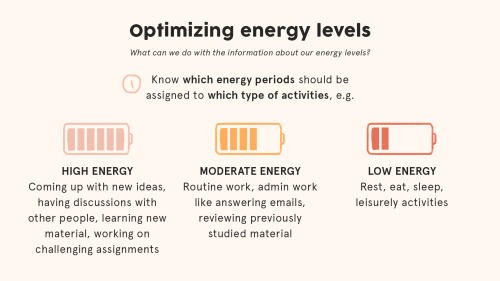
Energy Management

A human-based organization method

click on images for better resolution; images also available here (link to google drive)

Other posts that may be of interest:

Getting stuff done: How to deal with a lack of motivation

Flexible time-blocking: A more breathable way to get things done

The ABCDE Method

haha of course, how silly of me

you really can't

wha?

please explain what this message means or else the curiosioty will kill me

me when Čech cohomology

i love math. i hate math. i can do it all day, everyday. i cannot solve a single question. it's my favorite subject. I would rather kms than open the book. it's beautiful and everything makes sense and it's the best. it's fucking useless and nothing is logical and it's the worst. it's the loml. it's my arch nemesis.

22 VIII 2022

I will have to give a talk soon, in a few days I'll be attending a student conference. I decided to prepare something about my latest interest, which is knot theory. what makes it so cool for me is that the visual representations are super important here, but on top of that there is this huge abstract theory and active research going on

I decided to talk about the Seifert surfaces. this topic allows to turn my whole presentation into an art project

other than that I'm studying euclidean geometry and unfortunately it is not as fun as I thought it'd be

my drawings are pretty, ik. but there is almost no theory

I had a thought that working through a topic with a textbook is a bit like playing a game. doing something like rings and modules, the game has a rich plot (the theory), and quests (exercises) are there to allow me to find out more about the universum. whereas euclidean geometry has almost no plot, consists almost solely of quests. it's funny cause I never played any game aside from chess and mine sweeper

commutative algebra turned out to be very interesting, to my surprise. I was afraid that it would be boring and dry, but actually it feels good, especially when the constructions are motivated by algebraic geometry

commalg and AG answer the question from the first course in abstract algebra: why the fuck am I supposed to care about prime and maximal ideals?

oh and I became the president of the machine learning club. this is an honor but I'm understandably aftaid that I won't do well enough

I'm stressed about the amount of responsibilities, that's what I wanted to run away from by having the holiday. good thing is I gathered so many study resources for this year that I probably won't have to worry about it anytime soon, or at least I hope so

I neglected this blog like hell, sorry

I had a lot of work to do, that's kinda what happened. but I would like to go back to posting regularly, so maybe I could write about something people would want to see?

for now my ideas for posts include

more study tips

a quick intro to moduli functors, since a lot of sources are written in a way that requires advanced algebraic geometry. I could explain the basics using (almost) only commutative algebra

updates on my life and what I've been working on

books recommendations

interesting math problems I encountered recently

if you'd like to see any of that, let me know! and feel free to give me more suggestions in the comments

this looks so great! I need to check this out as well

25 VIII 2022

I found the most beautiful math book I have ever seen

it covers the basics of algebraic topology: homotopy, homology, spectral sequences and some other stuff

one of the authors (Fomenko) was a student when this book was being published, he made all the drawings. imagine being an artist and a mathematician aaand making math art

just look at them

other than those drawing masterpieces there are illustrations of mathematical concepts

I'm studying homology right now, so it brings me joy to know that this book exists. I don't know how well it's written yet, but from skimming the first few pages it seems fine

I just finished watching a lecture about exact sequences and I find the concept of homology really pretty: it's like measuring to what extent the sequence of abelian groups fails to be exact

I'm trying to find my way of taking notes. time and again I catch myself zoning out and passively writing down the definitions, so right now I avoid taking notes until it's with a goal of using the writing as a tool for acquiring understanding. I'm trying to create the representations of objects and their basic relations in my mind at first, then maybe use the process of note-taking to further analyze less obvious properties and solving some problems

I will post more about it in the future, we'll see how that goes