Bsdndprplplld - You Can't Comb A Hairy Ball

Very funny when mathematicians call weird edge cases "pathological".

Mathematician looking at a function that's continuous everywhere but differentiable nowhere: yeah that function has something wrong with it.

Shortest math paper ever.

And with so much impact! It just disproved a widely accepted theorem from the year 1769 in 5 rows!!!

I'll never publish anything even remotely badass like this! But I want it so much!!!

I want you all to know that an Arab Muslim from Tunis proposed the Theory of Evolution near 600 years before Charles Darwin even took his first breath. Don’t let them erase you.

tips for studying math part 2:

studying for an exam but the course is super boring and you don't care about it at all, you just want to pass

start by making a list of topics that were covered in lectures and classes. you can try to sort them by priority, maybe the professor said things like "this won't be on the exam" or "this is super important, you all must learn it", but that's not always possible, especially if you never showed up in class. instead, you can make a list of skills that you should acquire, based on what you did in classes and by looking at the past papers. for example, when I was studying for the statistics exam, my list of skills included things such as calculating the maximum likelihood estimators, confidence intervals, p-values, etc.

normally it is recommended to take studying the theory seriously, read the proofs, come up with examples, you name it, but we don't care about this course so obviously we are not going to do that. after familiarizing yourself with the definitions, skim through the lecture notes/slides/your friend's notes and try to classify the theorems into actionable vs non-actionable ones. the actionable ones tell you directly how to calculate something or at least that you can do it. the stokes theorem or the pappus centroid theorem – thore are really good examples of that. they are the most important, because chances are you used them a lot in class and they easily create exam problems. the non-actionable theorems tell you about properties of objects, but they don't really do anything if you don't care about the subject. you should know them of course, sometimes it is expected to say something like "we know that [...] because the assumptions of the theorem [...] are satisfied". but the general rule of thumb is that you should focus on the actionable theorems first.

now the problem practice. if you did a lot of problems in class and you have access to past papers, then it is pretty easy to determine how similar those two are. if the exercises covered in class are similar to those from past exam papers, then the next step is obvious: solve the exercises first, then work on the past papers, and you should be fine. but this is not always the case, sometimes the classes do not sufficiently prepare you for the exam and then what you do is google "[subject] exercises/problems with solutions pdf". there is a lof of stuff like this online, especially if the course is on something that everybody has to go through, for instance linear algebra, real and complex analysis, group theory, or general topology. if your university offers free access to textbooks (mine does, we have online access to some books from springer for example) then you can search again "[subject] exercises/problems with solutions". of course there is the unethical option, but I do not recommend stealing books from libgen by searching the same phrase there. once you got your pdfs and books, solve the problems that kinda look like those from the past papers.

if there is a topic that you just don't get and it would take you hours to go through it, skip it. learn the basics, study the solutions of some exercises related to it, but if it doesn't go well, you can go back to it after you finish the easy stuff. it is more efficient to learn five topics during that time than to get stuck on one. the same goes for topics that were covered in lectures but do not show up on the past papers. if you don't have access to the past papers you gotta trust your intuition on whether the topic looks examable or not. sometimes it can go wrong, in particular when you completely ignored the course's existence, but if you cannot find any exercises that would match that topic, then you can skip it and possibly come back later. always start with what comes up the most frequently on exams and go towards what seems the most obscure. if your professor is a nice person, you can ask them what you should focus on and what to do to prepare, that can save a lot of time and stress.

talk to the people who already took the course. ask them what to expect – does the professor expect your solutions to be super precise and cuts your points in half for computation errors or maybe saying that the answer follows from the theorem X gets the job done? normally this wouldn't be necessary (although it is always useful to know these things) because when you care about the course you are probably able to give very nice solutions to everything or at least that's your goal. but this time, if many people tell you that the professor accepts hand-wavey answers, during the exam your tactic is to write something for every question and maybe you'll score some extra points from the topics you didn't have time to study in depth.

alright, that should do it, this is the strategy that worked for me. of course some of those work also in courses that one does care about, but the key here is to reduce effort and time put into studying while still maximizing the chances of success. this is how I passed statistics and differential equations after studying for maybe two days before each exam and not attending any lectures before. hope this helps and of course, feel free to add yours!

omg I want this so much, I could share my ideas and things I learned

I think tumblr should let us post diagrammes and graphs and tables. We can be trusted with math. I promiss.

in my country having a diagnosis is highly confidential, too. there is no such thing as "the government knowing about your diagnoses" unless you get evaluated for disability documentation (I have no idea how to translate this to english), which is your choice. besides, who knows when the diagnosis will be useful? waiting for a diagnostic appointment takes several months and is very expensive, so taking an opportunity to sort this thing out when it's possible is good. depending on where someone lives, it can be very harmful to say that having a diagnosis somehow creates disadvantages

at my university the support program for people with asd has been introduced two years ago. it took me almost a year to get everything done, a year of unnecessary suffering. treatment for depression with or wihout adhd can be completely different and having it on paper that in your personal circumstances ssri might not work can save so much time. when someone suspects adhd and the situation calls for introducing medication, it's nice to be able to try right away, not wait several months for a diagnosis. those are just some practical examples of how you never know when diagnosis might be useful

and the validation reason, yeah, that too, it's beneficial to have someone work with you through that stuff. moreover, with professional support there comes someone suggesting solutions and forms of help that one might not even thought of. there are shitty doctors, but there are good ones too, and I think we should talk more about how to find the right ones instead of demonizing getting help

By the way. Before you rush to get a professional diagnosis for a Brain Thing you should really weigh your options. Like do you just want to "prove it" or will this actually give you access to treatment you can't have otherwise? Are the treatment options available worth having the government know you're neurodivergent? Because sometimes it's better to keep things off the record because unfortunately we still live in a very deeply ableist society and you might not want to have more real material oppression stacked against you than you have to

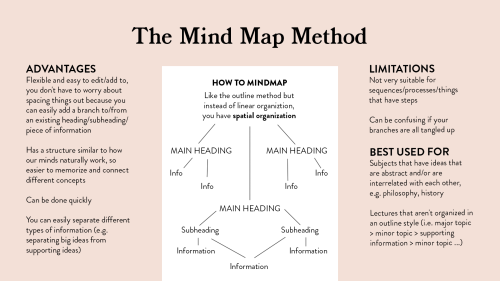
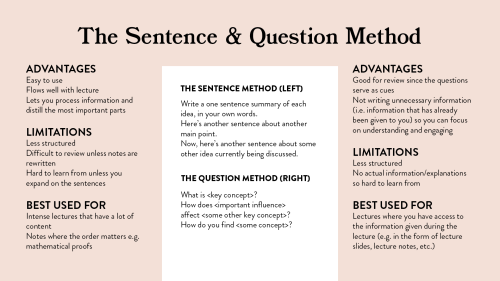
An Overview of Note-Taking Styles

Note-taking is one of the most essential skills a student should master. It allows you to record and review information to be used in the future. But what’s the best way to do so? Here’s an overview of note-taking styles that can help you maximize your learning!

I can relate to your undergrad experience! And I think it might be a good sign looking forward, because you've developed insights and ways of thinking and motivation to go beyond undergrad and seek out new spaces where you can do your own work. That's by no means common, I know many fellow undergrads who are a) as mystified when they retake a class as they were the first time round, and b) feel accomplished enough to have passed eg Introductory Analysis and have no drive to look onward. You seem to know very much what you're good at, what interests you and which areas you'd like to grow in. I'd argue that undergrad studies, which give you an introduction and overview of the field and teach basic reasoning skills while not expecting any really original problem solving aren't exactly made for people like you. Talking to your professors or Masters or even PhD students is a really good idea!

thank you for your input, it brings a huge relief!

I already talked to two of my professors and they said that there is nothing to worry about. my advisor said that in his opinion learning new concepts while working on some problem is the right way to learn and from his experience this is way more rewarding than learning for school or even "just to learn". he also said that if I'm interested in working more on open stuff then he will let me know when he finds some questions I could ponder. the other professor said that it's a good thing, because from his experience a lot of people tend to get discouraged when there is no way of knowing how long solving the problem will take or how much new theory is needed, and I seem to be the other way around, so the work I'll be doing in the future probably won't scare me as much

I talked to some of my friends who are about to finish undergrad like me, and there are people who feel the same way as I do. coincidentally, those are the people who had the same situation as mine, that is, they were lucky enough to find an advisor who gave them an open question to work on. other people I talked to seem to be fairly content with studying for the classes and completing homework assignments, and they didn't get to work on something open yet, so maybe it has something to do with getting the taste of the good stuff haha

I can see now that the future looks good and I'm motivated to go exploring. I am aware that I have so much more to learn, but having got the reassurance that I'm probably doing it right, it doesn't sound as scary anymore

chaotic good

Pro-tip: You can use paper twice if you take your notes in pencil first and then write over it in pen. 

@shitstudyblr please validate me