Fractal

😆😆😆

Mel Bochner, Untitled (“Child’s Play!”: ‘Study for 7-Part Progression’), (pen and black ink on off-white wove paper), 1966 [Art Institute Chicago, Chicago, IL. © Mel Bochner]

If one remembers this particular episode from the popular sitcom ‘Friends’ where Ross is trying to carry a sofa to his apartment, it seems that moving a sofa up the stairs is ridiculously hard.

But life shouldn’t be that hard now should it?

The mathematician Leo Moser posed in 1966 the following curious mathematical problem: what is the shape of largest area in the plane that can be moved around a right-angled corner in a two-dimensional hallway of width 1? This question became known as the moving sofa problem, and is still unsolved fifty years after it was first asked.

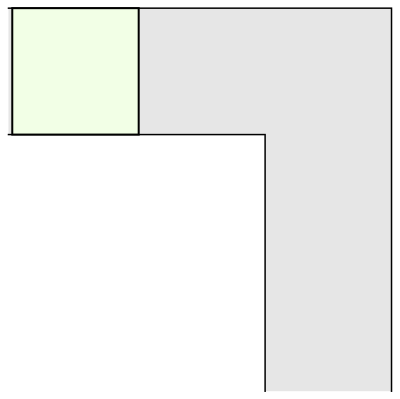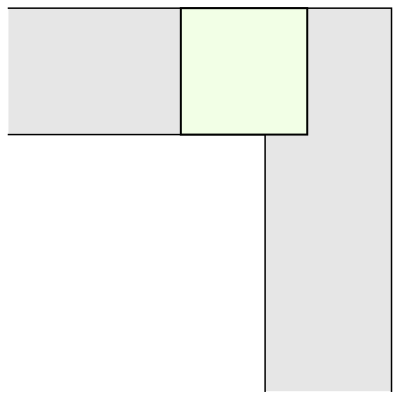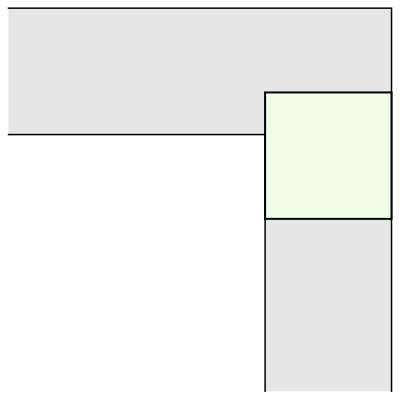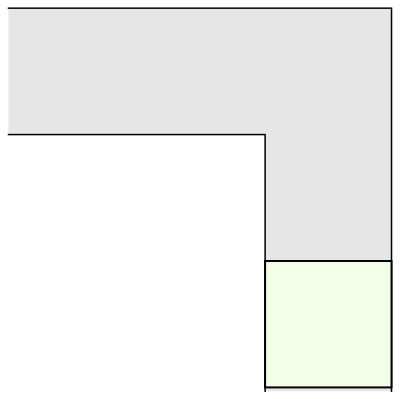
The most common shape to move around a tight right angled corner is a square.

And another common shape that would satisfy this criterion is a semi-circle.

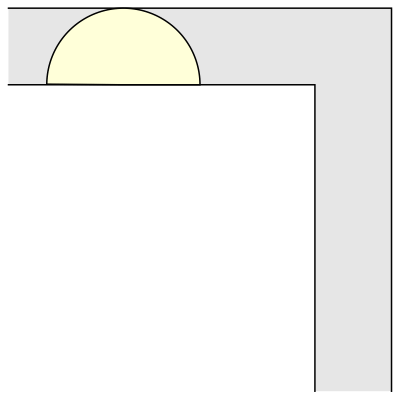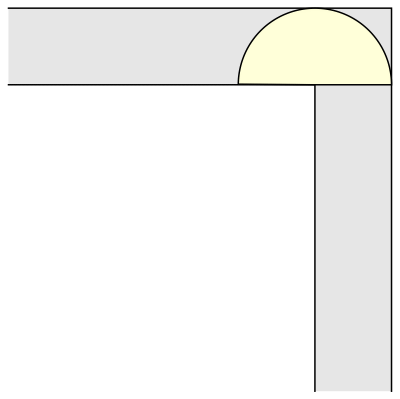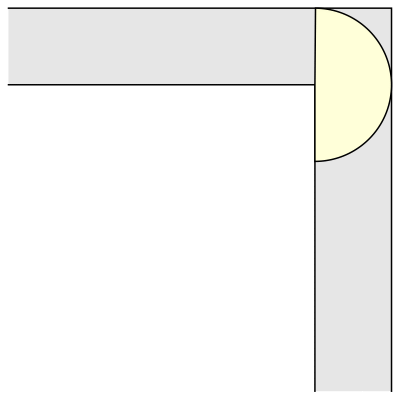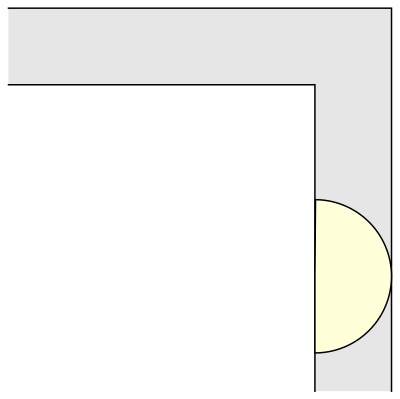
But what is the largest area that can be moved around?

Well, it has been conjectured that the shape with the largest area that one can move around a corner is known as “Gerver’s sofa”. And it looks like so:

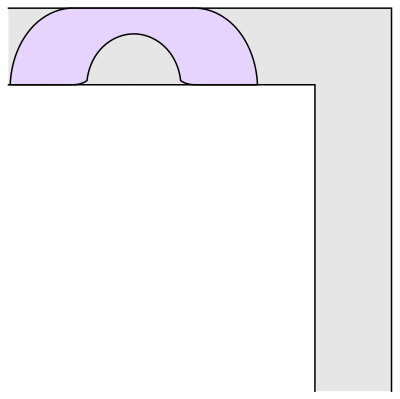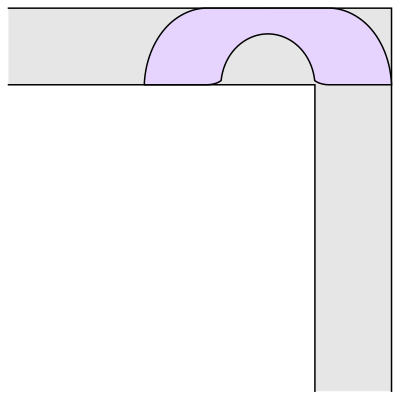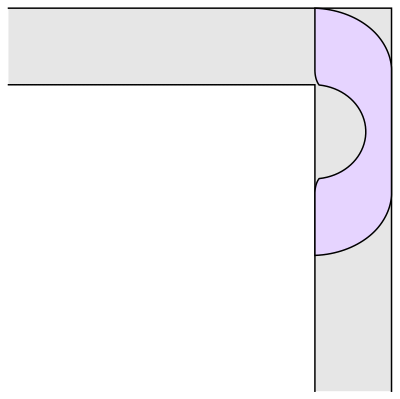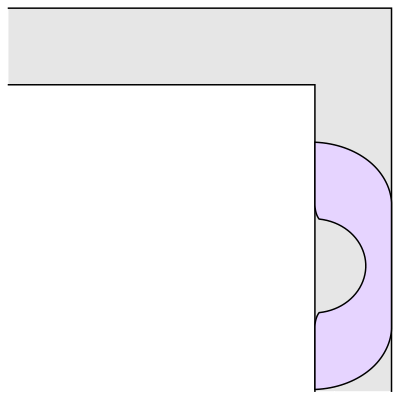
Wait.. Hang on a second

This sofa would only be effective for right handed turns. One can clearly see that if we have to turn left somewhere we would be kind of in a tough spot.

Prof.Romik from the University of California, Davis has proposed this shape popularly know as Romik’s ambidextrous sofa that solves this problem.

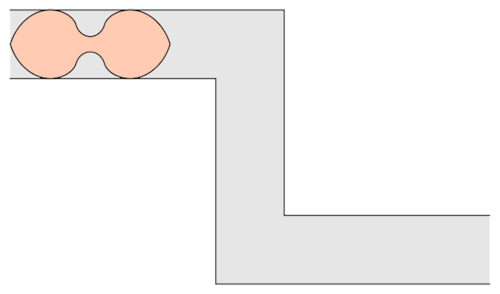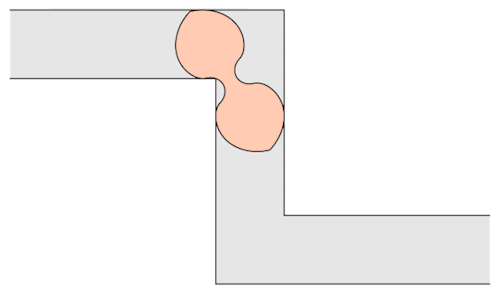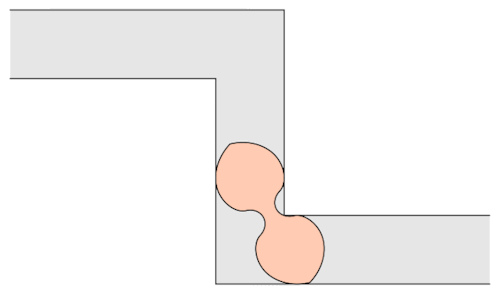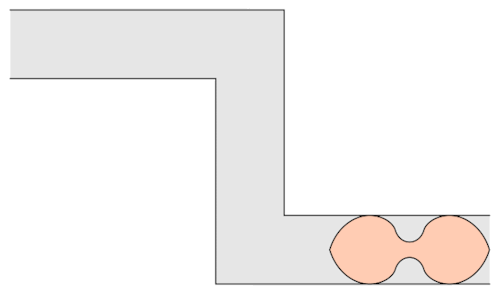
Although Prof.Romik’s sofa may/may not be the not the optimal solution, it is definitely is a breakthrough since this can pave the way for more complex ideas in mathematical analysis and more importantly sofa design.

Have a good one!

Basic definition of a tangent line.

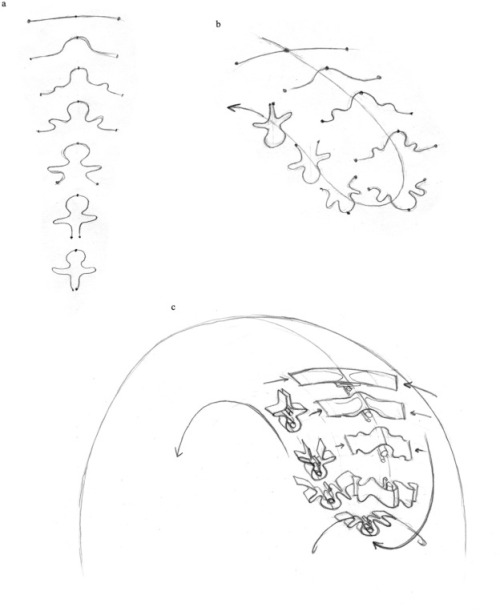
Embryo geometry: a theory of evolution from a single cell to the complex vertebrate body

24 “blueprints” that illustrate how the musculoskeletal, cardiovascular, neurological, and reproductive systems evolve through the mechanical deformation of geometric patterns. These images show how the vertebrate body might have evolved from a single cell during the evolutionary time and during individual development.

Though neither rigorous nor exhaustive in an empirical sense, our model offers an intuitive and plausible description of the emergence of form via simple geometrical and mechanical forces and constraints. The model provides a template, or roadmap, for further investigation, subject to confirmation (or refutation) by interested researchers.

The concept of “embryo geometry” suggests that the vertebrate embryo might be produced by mechanical deformation of the blastula, a ball of cells formed when a fertilized egg splits. As these cells multiply, the volume and surface area of the ball expand, changing its shape. According to the hypothesis, the blastula preserves the geometry of the initial eight cells generated by the egg’s first three divisions, which establish the three axes of the vertebrate body.

Though speculative, the model addresses the poignant absence in the literature of any plausible account of the origin of vertebrate morphology. A robust solution to the problem of morphogenesis—currently an elusive goal—will only emerge from consideration of both top-down (e.g., the mechanical constraints and geometric properties considered here) and bottom-up (e.g., molecular and mechano-chemical) influences.

Origin of the vertebrate body plan via mechanically biased conservation of regular geometrical patterns in the structure of the blastula, David B. Edelman, Mark McMenamin, Peter Sheesley, Stuart Pivar

Published: September 2016, Progress in Biophysics and Molecular Biology DOI: 10.1016/j.pbiomolbio.2016.06.007

The 120-cell. 

You probably think dodecahedra are tight. Have you considered trying hyperdodecahedra?

Great thanks to Professor Mark Crawford, who showed me this gem. It may take a little bit to shatter your consciousness, so please be patient. :)

Dodecaplex. Polydodecahedron. Hecatonicosachoron. Dodecacontachoron. Hecatonicosahedroid.

Mathematics is beautiful. <3

Inscribed in a grid of 2n-by-2n cells is a circle with diameter 2n - 1. How many cells include a segment of the circle?

The count grows simply as 8n - 4. How would you show that?

Pendulum and light. Via here

Simple. Coolllllll

hm  (via complex form)